Modulus of Rupture

The modulus of rupture measures the tensile strength of concrete beams or slabs.

The flexural strength of a slab of unreinforced concrete, a beam, or other structure measures stress and force it can endure without breaking or bending.

In this article you’ll learn:

So, if you’re ready to go with a modulus of rupture, this article is for you.

Let’s dive right in.

Introduction to Modulus of Rupture:

The modulus of rupture is determined by three- or four-point bending tests on plain concrete beams frequently used to calculate the uniaxial tensile strength of concrete.

 There are numerous standards for the execution of these tests, and they are simple to conduct (e.g., ASTM C78).

Over the past 20 years, numerous studies have looked into the bending of plain concrete beams using FEM and tensile softening material behaviour.

Only the first part of the softening curve controlled the rupture modulus.

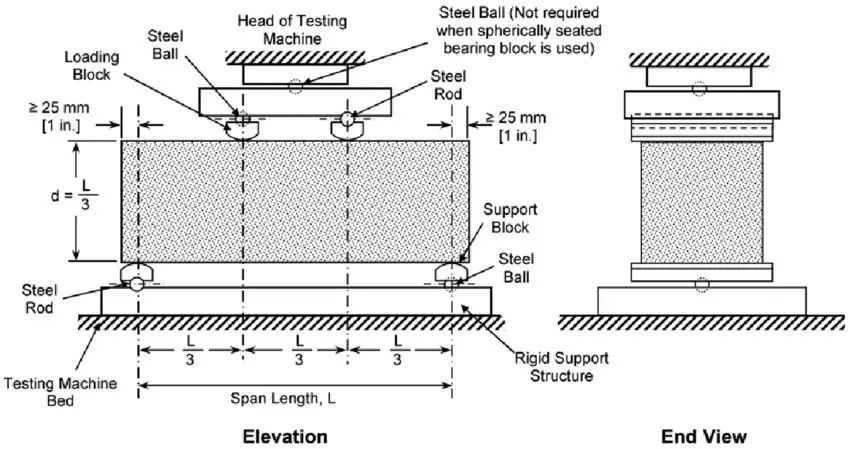
Standard Test Procedures for Modulus of Rupture of Concrete Beam:

Concrete beams must have span lengths that are at least three times their depths in order to be tested for their flexural strength.

The flexural strength is expressed as the MR in psi (MPa).

To determine a concrete beam’s flexural strength, there are two common tests:

1. Centre Point Loading Test (as per ASTM C 293):

During such a measurement technique, the entire load is applied in the center of the beam’s span length.

The flexural strength exceeds by the three-point bending loading test.

At the beam’s center the greatest amount of stress exists.

2. Third Point Loading Test (as per ASTM C 78):

At each third of the beam’s span length, the test method applies half the load.

In this instance, the flexural strength is lower than the rupture modulus discovered in the center point loading test.

The centre third of the beam is where the most stress is concentrated in this test.

The flexural modulus varies between 10 and 20% of the compressive strength depending on the type, size, and quantity of coarse aggregate used in a concrete beam.

Laboratory tests for the specified materials and mix design, yield the best correlation for particular materials.

It is determined by the third point loading up to 15% lower than MR, which is determined by centre point loading.

Calculation for Modulus of Rupture:

For various types of loading systems, the rupture formula varies.

 A rectangular sample subjected to a load in a three-point bending configuration:

Equation 1= (3FL)/(2bd2)

F represents the force (load) at the fracture point (N).

L stands for the support span’s length.

D is thickness, and b is width.

2. A four-point bending configuration is used to load a rectangular survey, and the loading span is one-third of the support span.

Equation 2: Modulus of Rupture = (FL)/(bd2)

F is the load (force) at the fracture point for a four-point loading.

L stands for the support’s length (outer) width is span, and thickness is span.

3. If the loading span is half of the support span, then the 4-point bend setup is used.

Equation 3: Modulus of Rupture = (3FL)/(4bd2)

4. If the load span for the four-point bend setup is neither 1/3 nor 1/2 the support span.

Equation 4= (3F[L-Li])/(2bd2)

Li is the size of the inner or loading span.

Rupture Vs Tensile Strength:

In any object, there is always a chance that some local flaws will exist.

An object has a tendency to “expand” when subjected to tensile stress and object’s fibers or regions are all subject to the same force.

In this situation, any weak areas could succumb and deform.

Equally, flexural stress exerts a force on an object in both the tensile and compressive directions.

The forces exerted on the objects’ fibres are not distributed uniformly.

The “extreme fibers” or the fibers closest to the object’s surface are typically subject to the greatest forces.

They are most susceptible to rupture or break.

Advantages of Modulus of Rupture:

1. We can build structural components like beams, cantilevers, and shafts by using the calculation.
2. It gives developers of dynamic building materials a parameter.
3. It functions as a tool for predicting the construction project’s resistance and durability.

Disadvantages of Modulus of Rupture:

1. The final strength is determined by flexibility, which equals the moment of bending in the fracture divided by a portion of the beam section in relation to the failure of the beams.
2. The third point is occasionally up to 15% determined by the centre point loading.

Applications of Modulus of Rupture:

• In structural mechanics, the calculation is important because it aids in the design of structural components such as beams, cantilevers, shafts, etc.
• It supports research into materials and their properties.
• Also, gives a parameter for the creation of stronger building materials.
• Flexural strength is a helpful measure of a structure’s construction quality.
• It is a tool for predicting an object’s resistance and durability.

Also read: Fineness Modulus of Fine Aggregate (Sand)

Conclusion:

The modulus of rupture is a unit for measuring pressure or force per unit area, it is calculated by scientists and engineers using a variety of pressure magnitudes.

Pascals, megapascals, and pounds per square inch or psi are two ways that it can be measured.