What is Tributary Area in Columns?

A Tributary area is a region that encircles a column that is enclosed by a panel centerline.

The tributary area method is used to determine the forces and static loads transported from floor slabs to columns.

Designers frequently add reactions of the beams framing into the columns or employ tributary areas in columns to transfer loads from slabs to columns.

In this article you’ll learn:

So, if you’re ready to go with it, this article is for you.

Let’s dive right in.

What is Tributary Area?

The tributary area is most typically utilized by designers to calculate the load transfer from the slab to the column and the responses of the column’s framing beams.

Due to their ability to securely transport a variety of loads from the structure to the ground below, columns and beams play a crucial role in construction.

The foundations carry the weight of the load to the earth’s solid surface when it hits the ground.

The column is subjected to a range of loads including environmental stresses such as wind, snow, and earthquake, as well as structure loads (dead loads), floor and beam weights, furniture, and equipment.

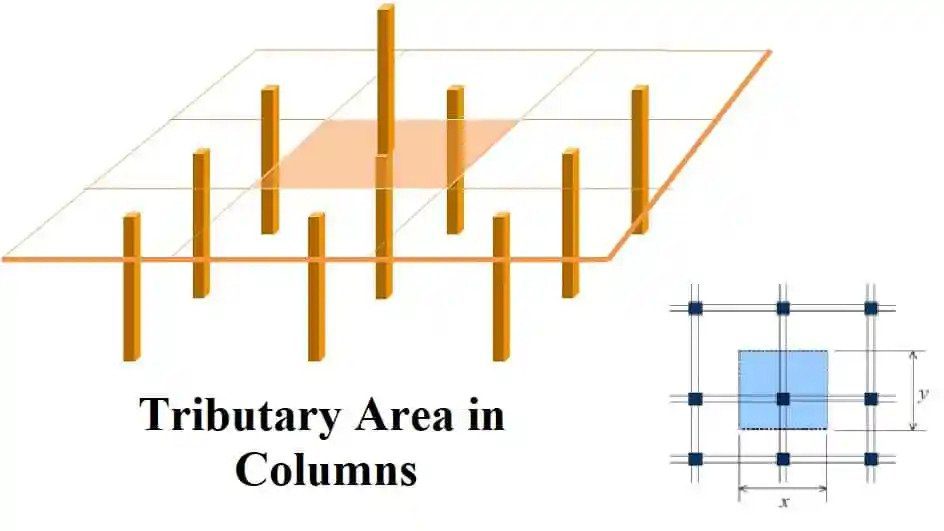
Tributary Area in Column:

The centre plane of the column is provided, where various properties are shown in the region surrounding the column as seen from the midline of the panel.

This is the column’s supporting region is provided in the area’s center to transfer the load.

The auxiliary field’s dead load per square inch is the same as the dead supported load constitutes a column’s tributary areas.

How to Determine the Area of a Tributary?

To calculate the precise tributary area, we must first comprehend how the forces move through the slab.

A stiffer column has a higher carry capacity to “transport” (or transfer) more forces, much as a broader river has more ability to transport water.

Also, the slab’s rigidity might vary depending on direction the beam, which causes the flow to be non-uniform.

This method determines which location on the slab is closest to the column.

This technique determines the position on the slab that is closest to the column at each specified point.

The territory on the side with the centerline column is known as its “Tributary area.”

Follow the Easy Steps below to Determine the Tributary Area:

Calculate the separation between the pairs of these two columns.
The separation between these two columns’ pair distances should be divided by 2.
In this technique, draw a line parallel to the centre.
Repeat each set of columns to create gridlines.

Example of Tributary Area:

Let’s use an illustration to better understand how to determine the tributary load of auxiliary areas.

Each of these sets’ midpoints is identified.
A perpendicular line is then drawn in accordance with it.
Thus, lines perpendicular to each column are drawn in front of them.

Let’s calculate Colum D-1 as a tributary area:

The neighbours of the column are first identified in each direction.
The D-1 column’s adjacent columns, c1, and d2 are identified.
Currently, the distance between D-1 and C-1 is specified as 16 metres, while the distance between D-1 and D-2 is specified as 8 metres.
The half distance between this column’s D-1 and C-1 will now be 16/2 meters or 8 meters, while the half distance between D-1 and D-2 will be 8/2 meters or 4 meters.
When using midpoints to help draw perpendicular lines.
Two drawn lines overlap in one place.
Column D-1’s location at an angle at this point establishes the angle of the auxiliary field.
The slab’s outer edge defines the other corners of the rectangle.
Since the boundary hatch is rectangular, we multiply to determine the side length.
Column D-1 = 8 x 4 = 32 M2 of tributary area is obtained.
Thus, the tributary load calculator can find the repeating procedure for all columns.